So my previous post looked at the maths behind Elo ratings and this post will go over how I’ve coded the rating system up in python. When I originally coded this up it was mainly to see how Elo ratings looked in the context of Prem rugby however now I plan to update them each week in light of the prem results and post predictions prior to each round. In terms of the code, in the words of Prussian field marshall Helmuth Karl Bernhard von Moltke: “No battle plan ever survives contact with the enemy.” What do I mean by this? I mean the code is probably going to change once the season starts as it was initially written to do a single piece of analysis but will need modified to make it easier to update on a weekly basis.
I’ll go over the initial implementation and how I calculated $k$ and home advantage constants.
The Code
1 - Import the required modules
import numpy as np
import pandas as pd
import requests
import os
2 - Create a class to parse and store a single seasons worth of results and fixture data
class SeasonData:
def __init__(self, season_start):
self.season_start = season_start
def parse_season_data(self, creds):
with requests.Session() as s:
s.post(URL, data=creds)
data = s.get(f'URL={self.season_start}')
self.season_df = pd.read_html(data.text)[3]
self.season_df.drop([1,5,7], axis=1, inplace=True)
self.season_df.columns = ['date', 'home_team', 'score', 'away_team', 'competition_round']
self.season_df = self.season_df.join(
self.season_df['score'].str.split(
' - ', expand=True
).rename(
{0:'home_points', 1:'away_points'},
axis=1
)
)
self.season_df['home_points'] = self.season_df['home_points'].astype(int)
self.season_df['away_points'] = self.season_df['away_points'].astype(int)
self.season_df.loc[self.season_df['home_points'] > self.season_df['away_points'], 'home_win'] = 1
self.season_df.loc[self.season_df['home_points'] < self.season_df['away_points'], 'home_win'] = 0
self.season_df.loc[self.season_df['home_points'] == self.season_df['away_points'], 'home_win'] = 0.5
self.season_df['date'] = pd.to_datetime(self.season_df['date'], dayfirst=True)
self.season_df.loc[self.season_df['home_win'] == 1, 'winning_team'] = self.season_df['home_team']
self.season_df.loc[self.season_df['home_win'] == 0, 'winning_team'] = self.season_df['away_team']
self.season_df.loc[self.season_df['home_win'] == 1, 'losing_team'] = self.season_df['away_team']
self.season_df.loc[self.season_df['home_win'] == 0, 'losing_team'] = self.season_df['home_team']
self.season_df.loc[self.season_df['home_win'] == 0.5, 'winning_team'] = 'DRAW'
self.season_df.loc[self.season_df['home_win'] == 0.5, 'losing_team'] = 'DRAW'
The above code creates a class which will scrape the season data from a certain website and create a pandas DataFrame with all the season’s data in the following format:
| date | home_team | score | away_team | competition_round | home_points | away_points | home_win | winning_team | losing_team | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2021-06-26 00:00:00 | EXETER | 38 - 40 | HARLEQUINS | Gallagher Premiership: Round 24 | 38 | 40 | 0 | HARLEQUINS | EXETER |
| 1 | 2021-06-19 00:00:00 | BRISTOL | 36 - 43 | HARLEQUINS | Gallagher Premiership: Round 23 | 36 | 43 | 0 | HARLEQUINS | BRISTOL |
| 2 | 2021-06-19 00:00:00 | EXETER | 40 - 30 | SALE | Gallagher Premiership: Round 23 | 40 | 30 | 1 | EXETER | SALE |
| 3 | 2021-06-12 00:00:00 | EXETER | 20 - 19 | SALE | Gallagher Premiership: Round 22 | 20 | 19 | 1 | EXETER | SALE |
| 4 | 2021-06-12 00:00:00 | BATH | 30 - 24 | NORTHAMPTON | Gallagher Premiership: Round 22 | 30 | 24 | 1 | BATH | NORTHAMPTON |
This dataframe will give us all the info we need for calculating the Elo ratings.
3 - Create a simple Team class containing the team name and their current Elo rating.
Note that any new team will start with an Elo rating of 1500:
class PremTeam:
def __init__(self, name):
self.team_name = name
self.elo_rating = 1500
4 - The next step is to create a class that can calculate and update Elo ratings:
class EloCalculator:
def __init__(self, home_advantage=75, k=40):
self.home_advantage = home_advantage
self.k = k
def update_single_fixture(self,fixture, teams):
"""
Update elo ratings for home and away teams
Parameters
----------
fixture: pd.DataFrame row
teams: dict {Team Name: PremTeam}
"""
home_rating = 10**((teams[fixture['home_team']].elo_rating + self.home_advantage)/400)
away_rating = 10**((teams[fixture['away_team']].elo_rating)/400)
home_expected_score = home_rating / (home_rating + away_rating)
away_expected_score = away_rating / (home_rating + away_rating)
home_win = fixture['home_win']
away_win = 1 - fixture['home_win']
winning_elo_diff = 0 if fixture['winning_team'] == 'DRAW' else teams[fixture['winning_team']].elo_rating - teams[fixture['losing_team']].elo_rating
margin_coeff = (np.log(np.abs(fixture['home_points'] - fixture['away_points'])+1) * 2.2) /\
(winning_elo_diff *0.001 + 2.2)
teams[fixture['home_team']].elo_rating += self.k * margin_coeff * (home_win - home_expected_score)
teams[fixture['away_team']].elo_rating += self.k * margin_coeff * (away_win - away_expected_score)
def predict_fixture(self, home_team, away_team, teams):
home_rating = 10**((teams[home_team].elo_rating + self.home_advantage)/400)
away_rating = 10**((teams[away_team].elo_rating)/400)
home_expected_score = home_rating / (home_rating + away_rating)
away_expected_score = away_rating / (home_rating + away_rating)
print(home_expected_score, away_expected_score)
return home_expected_score
The function update_single_fixture is just implementing the equations that I went over in my previous post. It takes as inputs a single row from the SeasonData table and a dictionary of PremTeam instances with the key being the team’s name and the value being an instance of PremTeam.
To explain, the code home_rating = 10**((teams[fixture['home_team']].elo_rating + self.home_advantage)/400):
fixture['home_team']is a returning the home team from the row of theSeasonDatarow that was passed to the function.teams[fixture['home_team']is then using this ‘home_team’ value to access the dictionary entry ofteamswhich will return an instance ofPremTeamfrom which we can read the elo_rating for a given team.
5 - We now need to write some code to bring all these classes together. I’ll go through it step by step.
# Create list of season dates for parsing season data.
# We'll be parsing all seasons from 2008 to 2020
season_dates = np.arange(2008,2021)
# Parse each season data and append to season_list
# Create an empty list to store all the seasons.
# For each season, scrape the season data and
# append the instance of SeasonData class to the list
seasons = []
for year in season_dates:
sd = SeasonData(year)
sd.parse_season_data(creds)
seasons.append(sd)
# Create list of all team names over parsed seasons.
# For every team that has a fixture in our data, add
# this team to the set of all team names
team_names = set()
for s in seasons:
for team in s.season_df['home_team'].unique():
team_names.add(team)
# Create a dictionary of all teams.
# The key is the team name and the value an
# instance of PremTeam class
teams = {}
for team in team_names:
teams[team] = PremTeam(team)
# Ensure that all the seasons are sorted in chronological
# order in ou list of SeasonData instances
seasons = sorted(seasons, key=lambda x: x.season_start)
# Instantiate the EloCalculator class
elo = EloCalculator()
# Iterate through all seasons
for season in seasons:
# Ensure the matches are in chronological order
df = season.season_df.sort_values('date')
# At the start of a season, revert each teams Elo ratings 1/3 towards the average
# to account for off-season changes. Bad teams ofetn get slightly better and
# good teams often sligthly worse so we regress everyone toward the mean to
# account for this
for team in teams:
teams[team].elo_rating = teams[team].elo_rating - np.abs((teams[team].elo_rating - 1500))/3 \
if teams[team].elo_rating > 1500 else teams[team].elo_rating + (np.abs(teams[team].elo_rating - 1500))/3
# Count the number of matches in the season
n_matches = df.shape[0]
# As we have sorted our SeasonData dataframe, we can access each fixture
# in order and update the each teams elo rating. The teams are stored in the
# dict called teams which we pass into this function
for i in range(n_matches):
elo.update_single_fixture(df.iloc[i], teams)
# Print the up to date elo_ratings
for team in teams.keys():
print(team, teams[team].elo_rating)
At the end of the 2019-2020 season, the Elo ratings ended up as follows (the teams are ordered by league position - note that Elo rating may not perfectly reflect league rating as it may depend on which teams a team beat/lost to):
- Wasps 1775
- Exeter 1731
- Bath 1647
- Bristol 1615
- Saracens 1572
- Worcester 1565
- Sale 1556
- Harlequins 1525
- Gloucester 1389
- Northampton 1318
- Leicester 1304
- London Irish 1215
6 - we also need to look at the best values for $k$ and $\mbox{HA}$.
The way we will do this is by calculating the mean squared error between our predictions and our outcomes. More formally:
\[MSE = \frac{1}{N} \sum_1^{\mbox{N}} (\mbox{Result} - \mbox{Prediction})^2\]# Parse the 2020-21 season data
sd2021 = SeasonData(2021)
sd2021.parse_season_data(creds)
# Drop any covide related cancellations
mask = (sd2021.season_df['score'] == '0 - 0') | (sd2021.season_df['score'] == '0 - 0')
sd2021.season_df = sd2021.season_df[~mask]
# Order values to iterate through seaason 1 round at a time
sd2021.season_df.sort_values('date', inplace=True)
# The teams Elo rating are based on fixtures prior to 2020-21 season, therefore
# prior to start of season, revert all elo ratings 1/3 toward the mean.
for team in teams:
teams[team].elo_rating = teams[team].elo_rating - np.abs((teams[team].elo_rating - 1500))/3 \
if teams[team].elo_rating > 1500 else teams[team].elo_rating + (np.abs(teams[team].elo_rating - 1500))/3
# Work through each match in the season. Calculate prediction for each match and updat elo
from copy import deepcopy
n_matches = sd2021.season_df.shape[0]
# Create a shallow copy of season_df for easier readability
df = sd2021.season_df
# Store a baseline of the teams dict which we can revert to
# everytime we use a new set of parameters
teams_baseline = deepcopy(teams)
# Create an empty dataframe to store the erros for
# each pair of parameters
rmse = pd.DataFrame(index=[10,20,30,40,50,60,70], columns=[*range(20,101,10)])
# Iterate through home advantage values 20,30...,100
for home in range(20,101,10):
# Iterate throguh k-values 10,20...,70
for k in range(10,71,10):
teams = deepcopy(teams_baseline)
elo = EloCalculator(k=k, home_advantage=home)
sq_error = 0
for i in range(n_matches):
prediction = elo.predict_fixture(df.iloc[i]['home_team'], df.iloc[i]['away_team'], teams)
sq_error += np.power(prediction - df.iloc[i]['home_win'], 2)
elo.update_single_fixture(df.iloc[i], teams)
# calculate error at end of season
error = np.sqrt(sq_error/n_matches)
# Insert error into dataframe
rmse.loc[k,home] = error
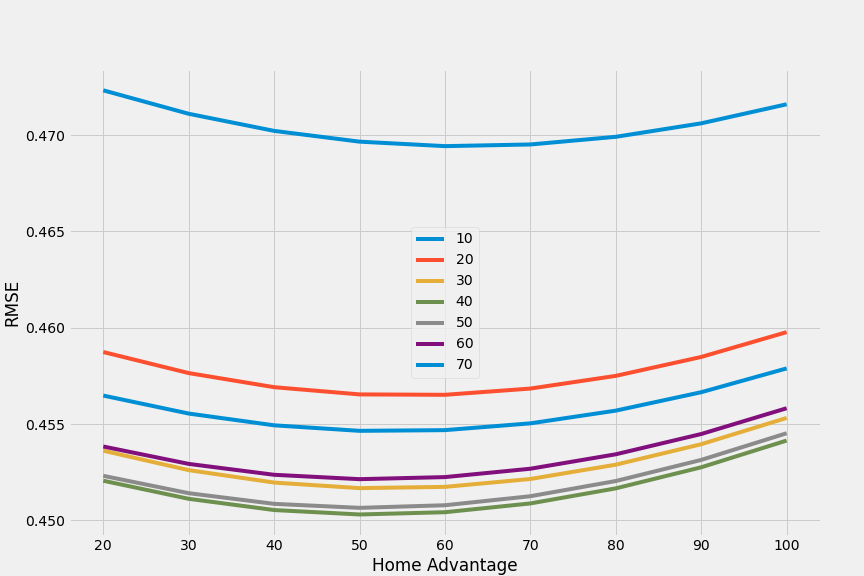
When we plot the output of the above we can see that the best values for $k$ and $\mbox{home advantage}$ are 40 and 50 respectively. It should probably be noted that home advantage may have had less of an influence in this season due to the lack of crowds but we’ll roll with it and see how it pans out over the current season.
7 - Finally, let’s plug the values for $k$ and $\mbox{HA}$ back into the whole thing.
I’ll run it from the start and see where each team will be starting from this coming season. The first value represents where they ended up at the end of 2020-2021 season and the second value is their starting value for this coming season after reverting each team towards the mean.
| Team | End of 2020-21 Season | Start of 2021-2022 Season |
|---|---|---|
| Bristol | 1657 | 1604 |
| Exeter | 1755 | 1670 |
| Sale | 1720 | 1647 |
| Harlequins | 1722 | 1648 |
| Northampton | 1414 | 1442 |
| Leicester | 1536 | 1524 |
| Bath | 1439 | 1459 |
| Wasps | 1391 | 1427 |
| London Irish | 1286 | 1357 |
| Newcastle Falcons | 1402 | 1434 |
| Gloucester | 1532 | 1522 |
| Worcester | 1146 | 1264 |
| Saracens | 1548 | 1532 |
Wrap up
This wraps up my post. I’ll start making predictions prior to the start of the season and we can see how accurate the Elo ratings are. Once we’re into the season and internationals start, I’ll consider revising the ratings depending on the number of international players missing amongst other things.
